Note that the dependence of uj, vj, wj on the spatial coordinate (x) makes the system infinite dimensional, leading to coupled ordinary and partial differential equations of motion.
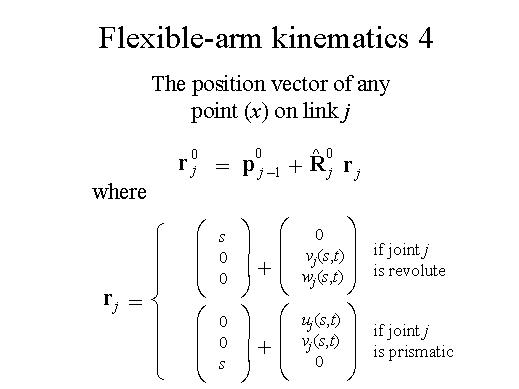
| The position
vector of any point (x) on link j with respect to the base
coordinate system (X0, Y0,
Z0) is expressed here, where uj(x,t),
vj(x,t), wj(x,t)
are displacements of the flexible link j as a result of flexibility
in respective directions. Note that the dependence of uj, vj, wj on the spatial coordinate (x) makes the system infinite dimensional, leading to coupled ordinary and partial differential equations of motion. | 
|