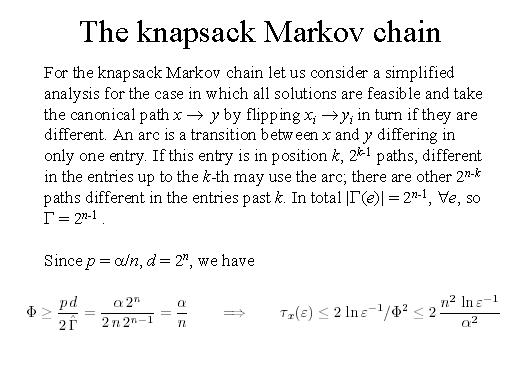For the knapsack Markov chain let us consider a simplified analysis for the case in which all solutions are feasible and take the canonical path x ® y by flipping x_i ® y_i in turn if they are different. An arc is a transition between x and y differing in only one entry. If this entry is in position k, 2^k-1 paths, different in the entries up to the k-th may use the arc; there are other 2^n-k paths different in the entries past k. In total |G(e)| = 2^n-1, "e, so G = 2^n-1. Since p = a/n, d = 2ⁿ, we have the following…