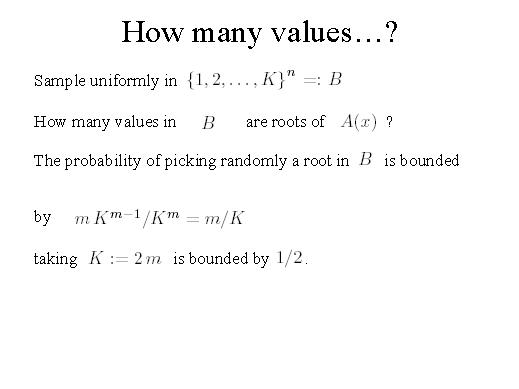Let m be the variables in det A(x) and let r_m the number of roots in B for a multilinear polynomial in m variables. If we arbitrarily fix the values of x₁,...,x_m-1 we get a first degree polynomial in x_m if the coefficient of x_m is non zero, and so there is at most one value of x_m which makes the determinant zero. This happens for every possible choice in B of x₁,...,x_m-1. Hence there are at most K^m-1 vectors in B which are roots of det A(x) if the coefficient of x_m does not vanish. If on the contrary the coefficient of x_m does vanish, and this can happen at most r_m-1 times because the coefficient is a polynomial in _m-1 variables, the value of x_m is irrelevant and so there are at most r_m-1K roots. Then r_m £ K^m-1+ r_m-1K with r₁ £ 1. One gets easily r₂ £ 2K and in general r_m £ mK^m-1.
The probability of picking randomly a root in B is bounded as follows.