In decision-making problems, one is often faced with making decisions based upon phenomena that have uncertainty associated with them. This uncertainty is caused by inherent variation due to sources of variation that elude control or the inconsistency of natural phenomena. Rather than treat this variability qualitatively, one can incorporate it into the mathematical model and thus handle it quantitatively. This generally can be accomplished if the natural phenomena exhibit some degree of regularity, so that their variation can be described by a probability model. The ensuing sections are concerned with methods for characterising these probability models.
Suppose the demand for a product over a period of time, say a month, is of interest. From a realistic point of view, demand is not generally constant but exhibits the type of variation alluded to in the previous section. Suppose an experiment that will result in observing the demand for the product during the month is run. Whereas the outcome of the experiment cannot be predicted exactly, each possible outcome can be described. The demand during the period can be any one of the values 0, 1, 2, …, that is the entire set of nonnegative integers. The set of all possible outcomes of the experiment is called the sample space and will be denoted by W.
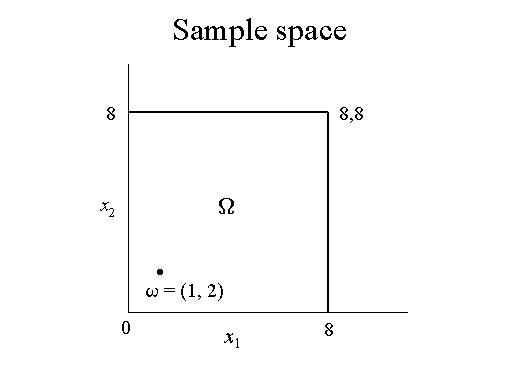
The set of all possible outcomes of the experiment W consists of all points (x₁, x₂), 0 £ x₁, x₂ £ 8, where x₂ represents the time first customer arrives on the second day. Thus W consists of the set of all possible points w, where w represents a point in two space lying in the square shown here.