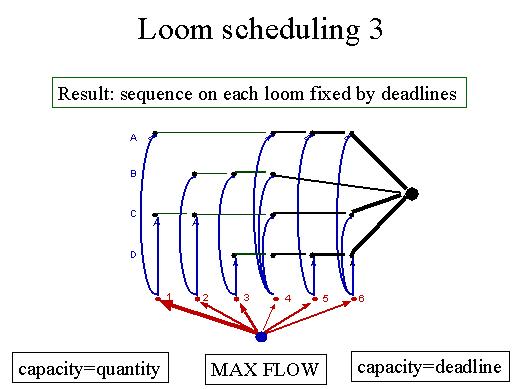
The basic result is that the sequence on each loom is fixed once we know the deadlines. This is very important because it allows a polynomial algorithm. Let's try to model the problem. So we have the different looms indicated as A, B, C, D and the various articles indicated as 1, 2, 3, 4, 5, 6. Here the sequence 1, 2, 3, 4, 5 and 6 is fixed by the deadlines. This means that article 1 has the strictest deadline an so on. Then we add a source and arcs from the source to each of the nodes referring to the articles. We assign to these arcs a capacity which is exactly equal to the quantity we want to have for each article. Then we send the quantity to the compatible looms, splitting it in a way which has to be determined. The quantity which arrives at a certain loom goes further on the horizontal arcs. These arcs are bounded by a capacity computed from the deadline. You may notice that in one case capacities correspond to quantities and in the other case to deadlines, that is to times. But quantities and deadlines are very simply related if the machines are uniform. Then if we try to impose a particular deadline, we fix the capacities and see whether there exists a feasible flow. We simply have to find the max flow from the source to the sink and, if the maximum flow saturates the arcs incident to the source, we are able to complete the jobs within the deadlines. If so, then we may decrease the deadlines and so on.

---