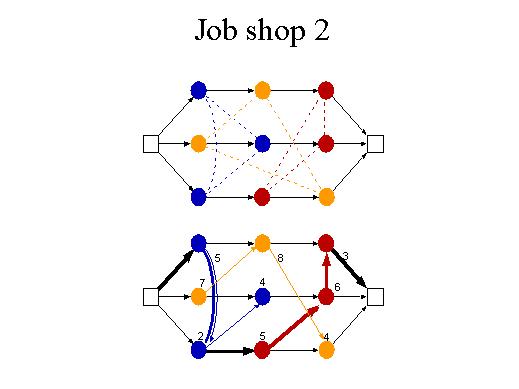
A possible combinatorial description of the problem is given by this graph where each chain corresponds to a job. Each operation is associated to a node of the graph and the arcs define technological precedences for the operations of each job. The node colours refer to the machines, so that the operations with the same colour have to be processed by the same machine. Moreover, since operations on the same machine cannot be processed at the same time, we have to insert precedences between operations associated to the same machine. We have many ways to do this, too many actually, and this is the very problem. In the first picture the dotted arcs represent precedences whose orientations have to be decided. In the second picture a possible choice is shown. The processing times translate into arc lengths and finding the minimum completion time amounts to finding the longest path in the graph, also called the critical path. With the indicated values of the processing times the heavy arcs represent the longest path.