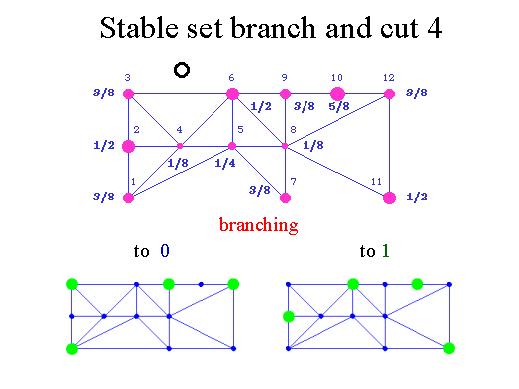
If we branch to zero, we get the solution here, which is integral these four nodes. If we branch to 1, we get another integral solution, which is with four nodes. So this is the maximal solution and we only needed a branching of two. This does show the power of branch-and-cut. This is the conclusion and we have that combining together the ideas of polyhedral combinatorics, finding facet defining inequalities together with branching is a really powerful technique to solve also very difficult problems.