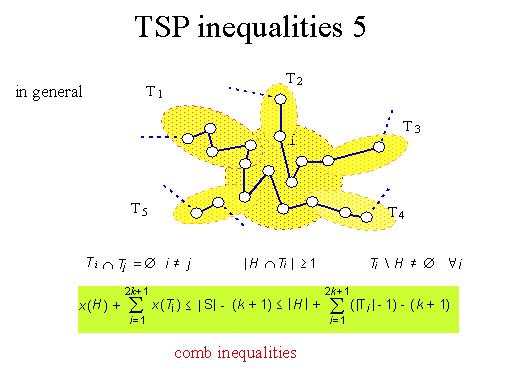
In general, what we may end up is something like this picture. We identify
a set of nodes called the handle, some sets of nodes called teeth (like
a comb), and we realise that the values on this set for all tours obey
these rather complicated inequalities, which of course cut the previous
fractional solution. These are called comb inequalities just because they
resemble a comb. And they are very effective in cutting off more fractional
inequalities. However even these inequalities are not enough, so that
for some problems we have to resort to branching if we are not able to
detect violating inequalities.
So we have to minimise the following Euclidean instance. First we get
these three sub-tours. Then by adding sub-tour inequalities, we get this
solution where the red lines are value one-half. We recognise here one
comb inequality, then we recognise a second comb inequality and by adding
these comb inequalities we get this new