So we have enlarged the set of inequalities. We realise that this is an exponential number of inequalities. However, this time this is not enough to describe the convex hull of tours.
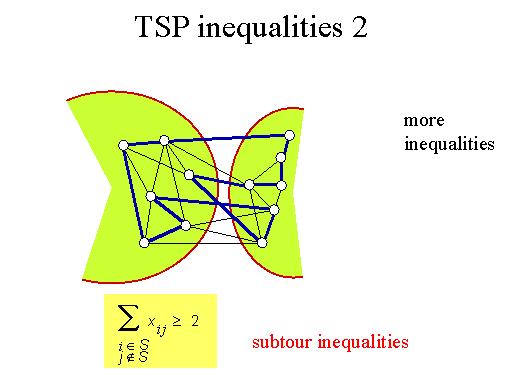
| So in order
to find these more inequalities let's consider a cut-set. In the cut-set
certainly there is one arc crossed by the tour in one way and there must
be another arc crossed in the reverse way. In certain cases we may have
more than two crossings. Certainly an even number, but in any case the number
of arcs in a generic cut-set used by any tour is greater or equal to two.
So, if we consider the following inequality, it is certainly valid for all
possible cut-sets of the graph. These are called sub-tour inequalities.
So we have enlarged the set of inequalities. We realise that this is an exponential number of inequalities. However, this time this is not enough to describe the convex hull of tours. | 
|