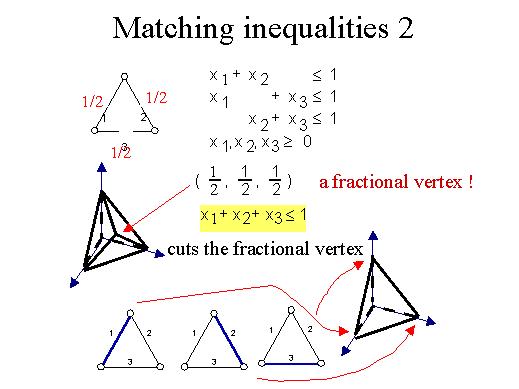
Now, to understand the answer to that question let's consider this small graph with three vertices and three arcs. Then the degree constraints are the ones described. However, the polyhedron in dimension three for these three inequalities is this one. And we recognise the four vertices which correspond to the matchings for each arc plus the empty matching. However, there exists one vertex here which has fractional coordinates: 1/2, 1/2, 1/2. Indeed, we see that the solution one-half is feasible for this subset. So this is a fractional vertex, and has nothing to do with a matching. How can we get rid of this situation? Well, we may think of cutting this fractional vertex by adding some inequality. In this simple case, we know that in a clique of three arcs, not more than one can be a matching, so we simply say that the sum of the three variables must be less than or equal to 1. What is the result after adding this cut? Indeed, this polyhedron has been transformed into this one, and here we can see that all possible four vertices correspond to matching.