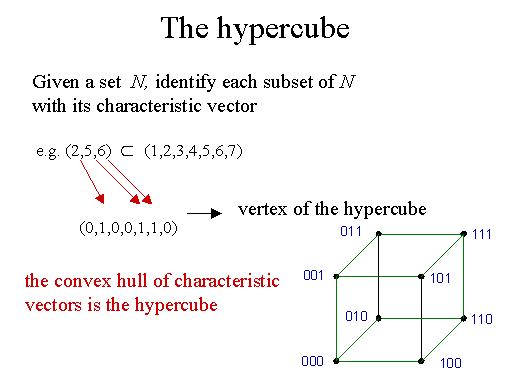
This lecture is concerned with results for particular problems arising in combinatorial optimisation. These results are aimed at finding inequalities to strengthen the description of the problem. The previous lecture was concerned with general integer linear programming problems. Now we have particular problems whose structure enables to find inequalities of particular type. So, let's first start with some basic results in polyhedral combinatorics. Results which are simply but useful to pave the way toward more complex results. First, let's consider a simple problem: we are given a set N and we want to identify each subset of N with its characteristic vector. Take for instance this subset, then we build up this incidence vector and each 1 is in correspondence with an element in the subset. Then we realise that this is a vertex of the hypercube. And we know that the convex hull of all characteristic vectors in this case is exactly the hypercube. This is the example in dimension three.