Given an integer linear programming problem and its feasible set S, denote
by P(S) the convex hull of S, which is the minimal convex set containing
S. A basic result states that if S is not empty, then P(S) is a polyhedron
whose vertices are elements of S and whose extreme directions are the
same ones of the underlying polyhedron P.
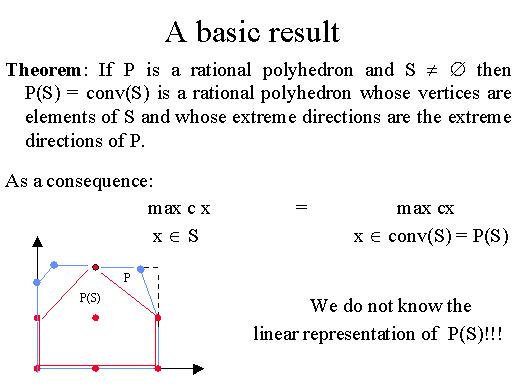
For instance in the figure, P is the polyhedron delimited by the blue
edges and, colored in red are its integer points, that is to say the elements
of the set S. If we design the the convex hull of these points we get
the polyhedron P(S) delimited by red edges.
As a consequence of the theorem, to optimize a linear function on the
discrete set S is equivalent to optimizing the same function on the polyhedron
P(S). Indeed a basic property of linear programming garantees that at
least one optimal solution of the second problem, if any exists, is a
vertex of P(S) and thus, by the previous theorem, an element of S. Unfortunately,
in general we do not know the linear representation of P(S), that is we
do not know how to represent P(S) by means of linear constraints.