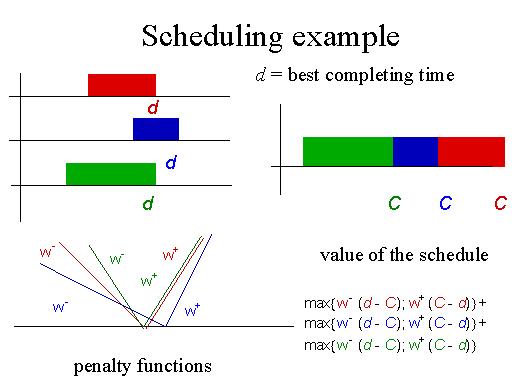
Now I show two formulations for the same problem. This is a scheduling problem with three jobs and we want to show how one formulation gives a bad lower bound and another one gives a good lower bound. In this problem we have three jobs for the same machine and there is a duration of each job. The jobs are depicted by red, blue and green. There is a best completing time for each job. The machine can process only one job at a time and without interruptions. So they cannot overlap in time and they have to be shifted a little bit with respect to the most desired completing time. We penalise both for being tardy and being early. So these are the penalty functions and for instance, if this is a possible schedule with three jobs in sequence, then the value of this schedule is given by this expression which makes use of the actual completion time and the best completion time. We want to minimise the sum of this maxima.