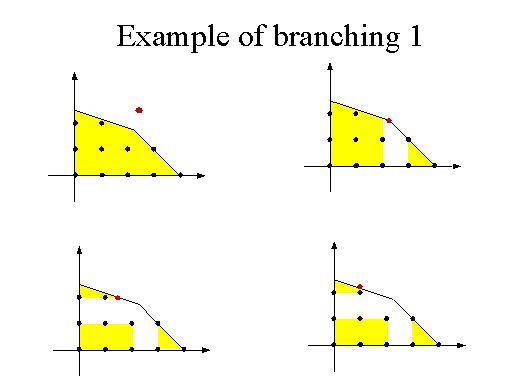
Let's see here an example of branching. The yellow set is the feasible set without integrality, and the blue dots are the integral points. Suppose we get the red dot as an optimum for a certain objective function. But this is fractional and so we have to partition the set into the two yellow regions. This way we avoid the white region without loosing any of the blue spots. Then we re-optimise and we find a new point, different from the previous one. This new point is clearly fractional and then we subdivide the feasible set again into the yellow regions. We eventually find this point and what we get here is a partition of the integral region into convex sets such that this polyhedron here is the convex hull of integral points.