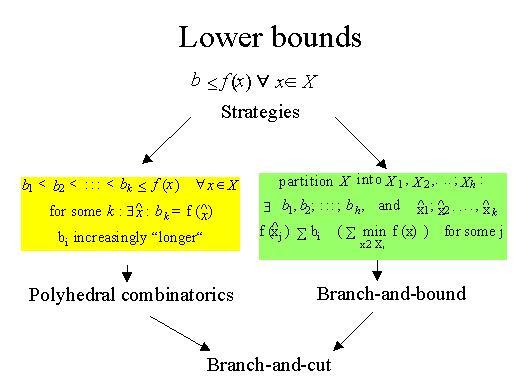
So, we want to find lower bounds of optimal solutions, that is something which is always less than the value of the function. Once we have lower bounds, the strategies we may adopt are basically of two types. Either you may find a sequence of lower bounds which are increasingly higher and hope to find eventually some points such that the lower bound is attained (but clearly what we expect is that the lower bounds are increasingly longer in term of string descriptions) or we may partition X into several sets, find the lower bounds within the sets, and hope also to find these particular solutions with inequalities attained as equalities. The first strategy leads to polyhedra combinatorics whereas the second leads to the perhaps more familiar branch-and-bound methods. Recently both strategies have been combined into a very powerful technique called branch-and-cut.