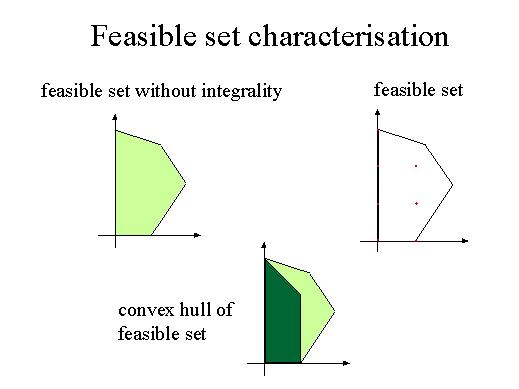
Let's see first what the feasible set is without the integrality constraint. Consider a polyhedron in R2 and the integral points within the polyhedron, these red dots, and we see that the feasible set has dramatically changed. A convex set of the plane has changed to a finite number of discrete points. We are particularly interested in finding the convex hull of the feasible set, i.e. the convex of the red points. To be able to determine this convex hull is one of the major tools in solving integer linear programming.