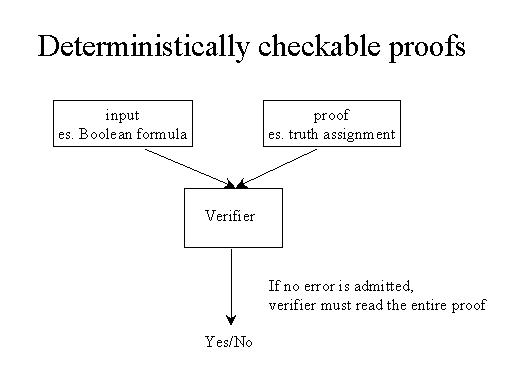
Let us assume that we have a Boolean formula as an input, and I want to convince you that this Boolean formula is satisfying. The simple way I have to convince you that this formula is satisfying is to give you a truth assignment.
Once I write down a truth assignment, you who are the verifier can read the formula, read the truth assignment and check whether the truth assignment satisfy the formula.
If you do not admit any error you have to read of course the entire proof. But what happens if you do not want an answer which is 100% correct? This lead us to another problem which is probabilistically checkable proof.