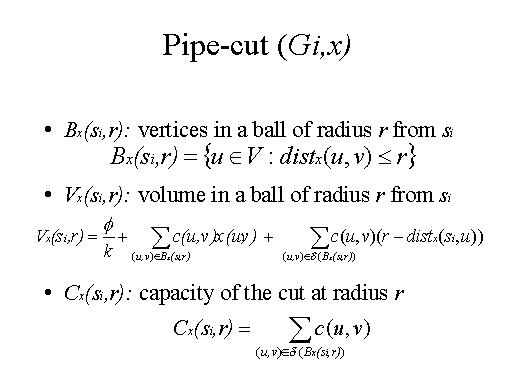
The procedure pipe cut does the following: we select a ball of radius R around a vertex si that is all the vertices in the ball are at distance at most R from si. We had to pick the right R in a way that the cost of disconnecting si, i.e. the cost of the capacity of the edges on the border of the ball is not too big. We compute the volume in the ball of radius R. This volume is given by the extra volume that we give to any source vertex F/k plus the total volume of the pipe system inside the ball plus the volume of the pipe system on the border of the ball. In particular, the capacity of capacity of the pipe system of the edges that cross the border can be proved to be the derivative of the volume with respect to the radius r.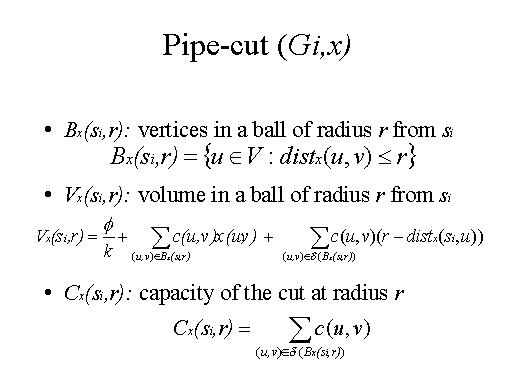

---