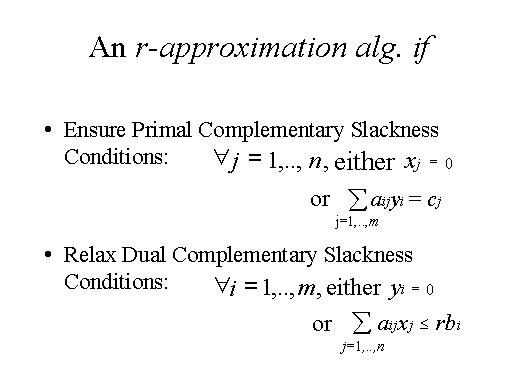The observation of the complementary slackness conditions allow to determine the approximation ratio of the primal-dual algorithm. This is a direct consequence of what it is called the strong duality theorem, that gives sufficient and necessary conditions because a x and y are optimal solution for the primal and for the dual. We have an r-approximation algorithm if, when we have finished the execution of the algorithm based on the primal-Dual Schema, we ensure the primal complementary slackers conditions that says that for every j either variable xj is equal 0 or the constrains in the dual are satisfied with equality. We relax the dual complementary slackness conditions and say that for every i either yi is equal 0 or the constraint in the primal is satisfied up to a factor r.

---